Play Sudoku HowTo Solve Sudoku HowTo Use Sudoku Online

Sudoku principles.

Rule of sudoku

A classical sudoku game goal is to fill board of 9x9 cells with numbers from 1 to 9 so that each group (row, column and 3x3 box) contains every number. As the consiquence a number cannot be present twice in a group. There are also variants with 4x4, 6x6, 12x12 and 16x16 boards. Also, especially for children, any set of different pictures or symbols may be used instead of numbers.

Solving Strategies

Here are some of strategies to solve sudoku in full mode. To illustrate examples cells are called in a form rycx so that r3c6 means cell in third row from the top and sixth column from the left.

Simplest strategies

These methods of solving sudoku are simplest but play very important role in solving sudoku since them finally put values to cells while more advanced techniks only eliminate candidates.

Naked single

If there is only one candidate for a cell value then this must be the value of the cell.

naked single

In this example for a cell r6c4 the only candidate is 2 so we may assign value 2 for the cell.

Hidden single

If there is only one candidate within a group for a certain value then this must be the value of the cell.

In this box only one cell has a 5 candidate so that cell must be 5.

Simple strategies

Naked pair

Naked pair is a generalization of naked single. If in some group are two cells with only two candidates that are the same for both cells then all candidates with those values from other cells of the group may be eliminated.

In this box candidates in two bottom cells are 5 and 6 so if one cell is 5 the other is 6 and vice versa. In either case upper cells in the box cannot be 5 or 6, so candidates 5 and 6 marked with red can be eliminated.

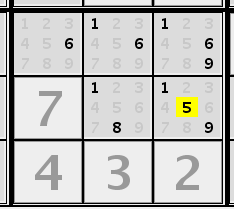
Naked subsets (triples, quads)

Triples, quads etc. are geniralization of naked singles and pairs.

naked triple

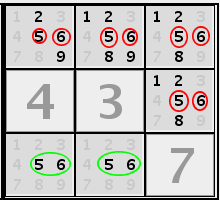
In this row cells 1, 3 and 6 have candidates only from 1, 4, 8. It doesn't matter that in cell 3 candidate 4 not present. In any case all 1, 4, 8 values must be at cells 1, 3, 6 so other cells cannot contain values 1, 4, 8.

Hidden subsets (pairs, triples, quads)

Hidden subsets are generalization of hidden singles and on the other hand complimentation of naked subsets. Lets look one more time at the row from naked subsets section. Candidates 2, 7, 9 are present only in cells 4, 7, 8. So other candidates (namely 1, 4, 8) from cells 4, 7, 8 are irrelevant. Its obviously that if in some group are n cells not solved and k cells form naked subset then other n-k cells form hidden subset.

Intersections

If all candidates for some value in a group lay within intersection with other group then all candidates for that value from other cells of second group may be eliminated.

intersection

All candidates 1 for left middle box are on row 5, so other candidates 1 for row 5 (in right middle box) may be deleted. This form box-line intersection.

All candidates 1 for row 5 are on right middle box, so other candidates 1 for right middle box (in row 5) may be deleted. This form line-box intersection.

It is not neccessary to form box-line and line-box intersection at the same time.

Fish strategies

X-wing

X-wing is a pattern of two rows contatain two candidates each for some value on the same two columns. In this case all other candidates for the value from other rows on the columns may be eliminated. Obviousely its true for two columns contains two candidates for value on two rows.

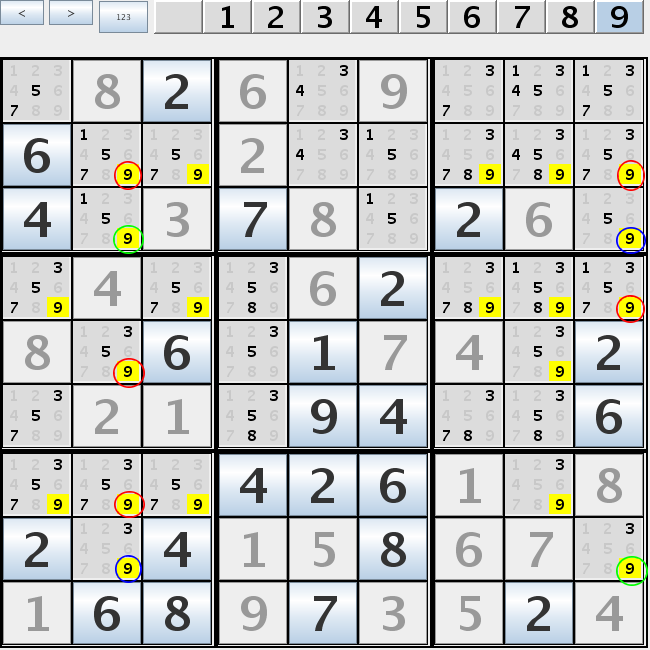
x-wing

In this example if r3c2 is 9 then r8c2 isn't 9 and r8c9 is 9. If r3c2 isn't 9 then r3c9 is 9 r8c9 isn't 9 and r8c2 is 9. In either case all 9 marked with red are eliminated.

Swordfish, jellyfish etc.

Swordfish and jellyfish are generalizations of x-wing for 3 and 4 rows/columns. n-fish for rows are complimented with r-f-n fish for columns, where r - size of board, f - number of already filled cells for a value. For classical sudoku with r=9 for all n-fishes with n>4 are always complimented with fishes with n<=4.

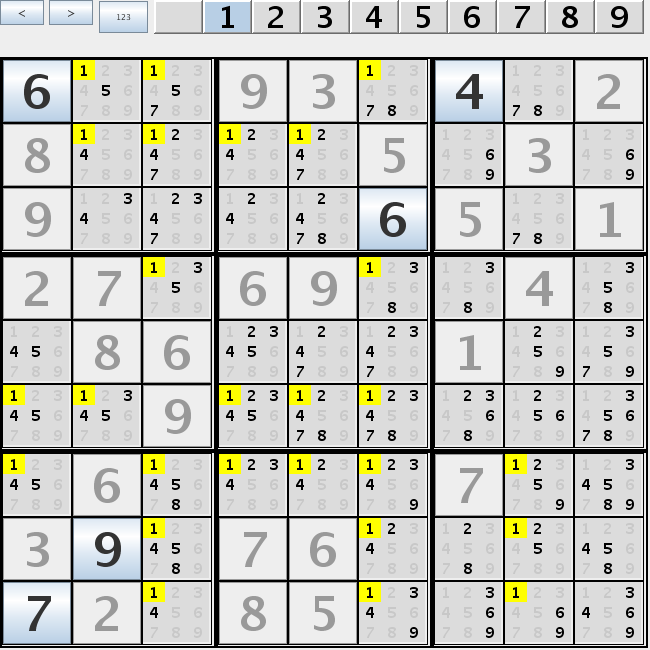
swordfish

In this example on columns 1, 4, 5 candidates for 1 are on rows 2, 6, 7 only. All candidates for 1 on rows 2, 6, 7 not from rows 1, 4, 5 (namely r2c2, r2c3, r6c2, r6c6, r7c3, r7c6, r7c8) can be eliminated.